在動力和航空航天等領(lǐng)域,設(shè)備一般都有復(fù)雜曲面和自由曲面零件,既要求有很高的幾何精度,還對加工表面形貌特征和物理性能有要求,而提高精度最重要的是加工過程誤差(主要是熱誤差和力誤差)和幾何誤差因素。現(xiàn)有的誤差測試與分離技術(shù)測試過程復(fù)雜,費時且成本高,大多是間接測試機床而非直接測試工件,生產(chǎn)現(xiàn)場很少采用。Denavit和Hartenberg[3]于1955年建立了著名的D-H法,是分析運動機構(gòu)在空間運動姿態(tài)的有力工具。Srivastava等[4]在一臺RRTTT型的五軸機床上建立了基于HTM方法的綜合誤差模型,在分別得到幾何誤差和熱誤差元素之后,可計算出各進給軸的補償量,對機床的空間誤差進行補償。天津大學(xué)劉又午教授[5]將多體系統(tǒng)理論引入數(shù)控機床建模,并對誤差辨識應(yīng)用9線法進行解決。
國防科技大學(xué)粟時平博士對機床多體系統(tǒng)運用拓撲結(jié)構(gòu)進行概括,并用低序體陣列進行描述,用特征矩陣表達了機床相鄰體之間的位姿,并以三軸、五軸機床為例給出了理想運動模型、有誤差運動模型和空間誤差模型等的具體表達式。上海交通大學(xué)楊建國等針對數(shù)控機床的誤差概念、誤差形成機理及誤差建模等進行了研究,并在誤差補償上有了重大突破。上海交通大學(xué)劉國良等開發(fā)了一種數(shù)控機床幾何誤差綜合建模專家系統(tǒng),可實現(xiàn)不同類型三軸加工中心的綜合誤差自動建模。東北大學(xué)劉春時等提出一套基于多體系統(tǒng)理論的五軸數(shù)控機床空間誤差建模流程,并以某VMC650高速銑削五軸加工中心為對象驗證了有效性。上海交通大學(xué)姜輝提出了一種熱誤差建模方法和誤差補償方法,并以FA-32M型銑床為研宄對象進行了驗證。清華大學(xué)李鐵民針對機床熱誤差建模進行了研究,探討了熱誤差建模的兩種方法(經(jīng)驗熱誤差建模和理論熱誤差建模)的優(yōu)缺點。北京航空航天大學(xué)劉強等提出一種適合機床動態(tài)分析的拓展傳遞矩陣建模方法,簡化了機床動力學(xué)建模過程,更適合工程應(yīng)用。
在特征樣件方面研究的領(lǐng)域很多,山東大學(xué)劉戰(zhàn)強提出了基于高速切削加工工件測試的誤差分離和誤差補償研究,但僅針對車床的加工樣件,且試驗只是定性試驗。哈爾濱工業(yè)大學(xué)趙磊等提出了基于特征樣件的方式來分離機床的幾何誤差研究,但僅考慮了幾何誤差,未針對加工誤差。湖南科技大學(xué)趙前程提出一種基于形狀誤差的特征模型,在誤差估計方法的準確度和不確定度上有很大優(yōu)勢,但僅從優(yōu)化方法上進行考慮。
本文基于特征樣件就幾何誤差進行分離,并可分離出加工過程誤差。在此方案中,應(yīng)用了在機測量系統(tǒng),避免工件二次裝夾,同時檢測、設(shè)計與加工過程緊密結(jié)合,有利于保證加工精度和降低廢品率。
2 誤差分離原理
加工工件的總誤差E一般將其定義為實際測量尺寸Drea與理想模型Dper之間的差值,即

加工后工件的實際測量尺寸很難達到理想值。
一般工件加工完成后會從機床取下,放置在三坐標測量儀上進行精度檢測,即進行離線測量。三坐標測量儀的測量精度一般高于加工要求的尺寸公差一個數(shù)量級,測得數(shù)值可看作實際尺寸Drea。
Mou和Liu經(jīng)試驗研究證明,工件加工后離線測量尺寸與在線測量尺寸的差異等于機床的定位誤差,當(dāng)試驗條件為室溫狀態(tài)時,此差異就是機床的幾何誤差,即
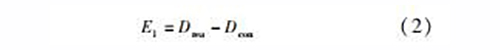
式中,Dcon為室溫在機測量所得數(shù)值。
3 機床幾何誤差建模
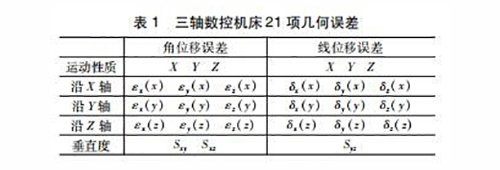
建立數(shù)控機床幾何誤差綜合模型,首先要分析機床的幾何誤差參數(shù),以大連機床VDL-1000E型數(shù)控銑床為例,共有21項幾何誤差參數(shù)(見表1)。
選擇測量點時,首先進入在機測量軟件,根據(jù)測量對象自動確定測量點選擇方式,生成待測量點,去除缺陷點,最后提取測量點信息。根據(jù)規(guī)劃好的測量點,測量各點的X、Y、Z坐標值來編寫測量程序。本文利用UG二次開發(fā)編寫在機測量軟件,并將其編入在機測量軟件中。
(1)建立三軸數(shù)控機床模型
圖1為該三軸數(shù)控機床的結(jié)構(gòu)示意圖,工件通過夾具安裝在X軸上,主軸安裝在Z軸上。
(2)建立拓撲結(jié)構(gòu)及坐標系
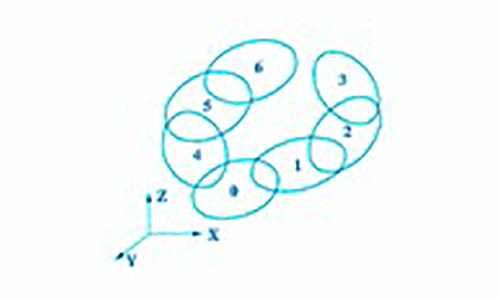
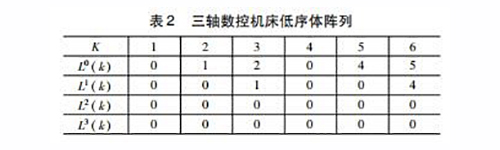
三軸機床的拓撲結(jié)構(gòu)如圖2所示,其低序體陣列見表2。首先在床身(慣性體0)上建立參考坐標系O0X0Y0Z0,然后按遠離床身的位置分別建立坐標系O1X1Y1Z1、O2X2Y2Z2、O3X3Y3Z3、O4X4Y4Z4、O5X5Y5Z5、O6X6Y6Z6。為了降低模型的復(fù)雜性,設(shè)坐標系OkXkYkZk(k=1,2,… 6)與參考坐標系O0X0Y0Z0重合。
(3)三軸數(shù)控機床的綜合誤差模型
為方便分析,建立機床運動鏈示意圖幫助理解(見圖3)。
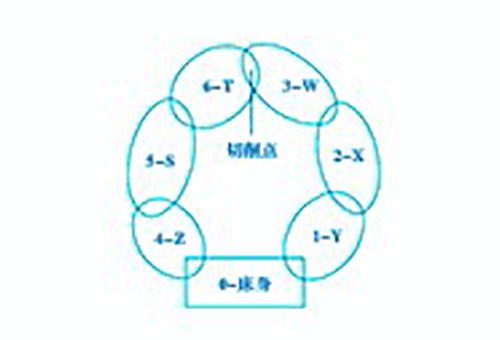
三軸數(shù)控機床空間幾何誤差綜合模型為
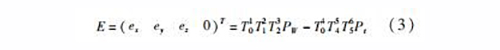
基于小誤差理論,略去誤差的二階以上項并對公式(3)進行化簡,得
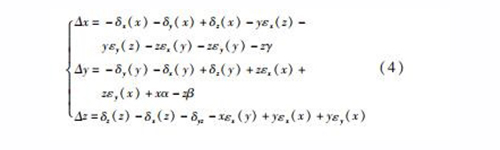
4 01203 建模仿真
使用MATLAB對公式(4)進行仿真。由圖4可知,x項綜合誤差隨y有小幅變化,隨x波動式的增加,在整個行程內(nèi)沿負方向呈遞增趨勢。由圖5可知,y項綜合誤差隨x有小幅變化,隨y波動式的增加,在整個行程內(nèi)呈遞增趨勢。如圖6所示,總誤差總體上隨著遠離設(shè)置的原點位置逐漸變大。



5 試驗分析
本試驗采用的數(shù)控加工系統(tǒng)為大連機床廠生產(chǎn)的立式數(shù)控加工中心VDL-1000E。在機測量系統(tǒng)作為測量時數(shù)據(jù)的記錄載體,基本參數(shù)如下:X行程1200mm、Y行程560mm、Z行程600mm,刀庫容量20把,主軸最高轉(zhuǎn)速為800r/min,定位精度全程±0012mm,重復(fù)定位精度為±0.008mm。采用應(yīng)用廣泛、功能全性能好的FANUC0i-MD系統(tǒng),并對外提供RS232外部控制接口,具有自己的宏編程語言,方便程序的編程調(diào)用。


測量的工件采用轎車覆蓋件的凸模進行試驗,驗證整個系統(tǒng)的通用性和測量精度。測量選擇轎車覆蓋件上的自由曲面部分進行測量,模具凸凹模的實體見圖7。
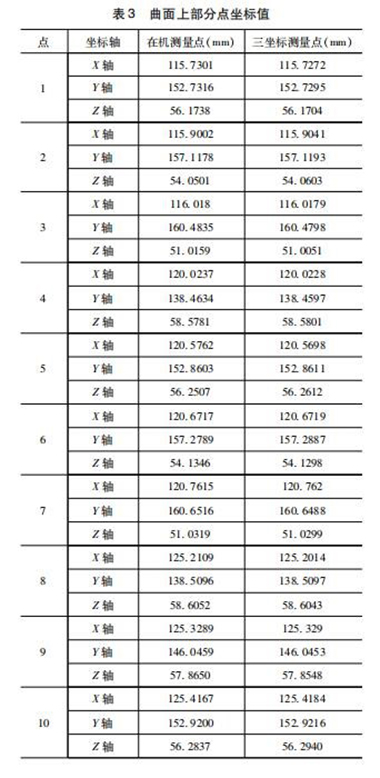
試驗數(shù)據(jù)對比:選取的數(shù)據(jù)點位置如圖8所示,采用在機測量和三坐標測量機測量所得數(shù)據(jù)整理后,曲面部分點坐標值數(shù)據(jù)見表3。
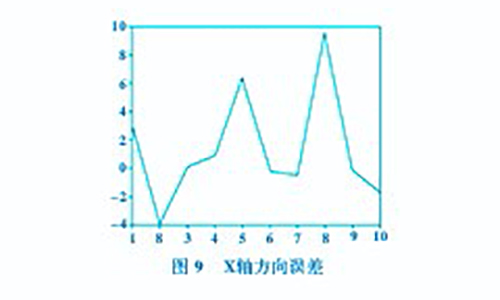
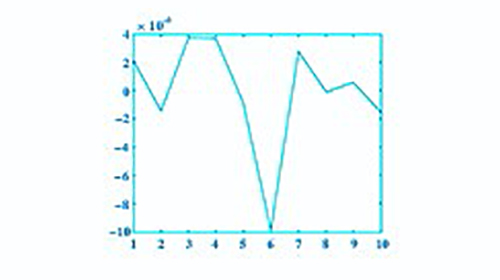
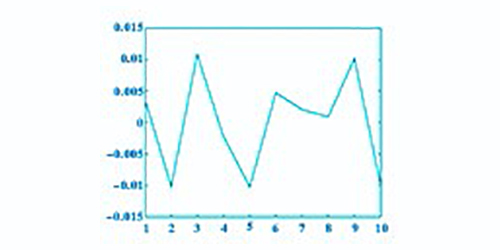
根據(jù)MATLAB軟件分析獲取的數(shù)據(jù),X、Y、Z軸方向的誤差分別如圖9、圖10和圖11所示。由實際數(shù)據(jù)測量得到plot圖,雖然選取的數(shù)據(jù)較少,但可以看出實際與預(yù)測趨勢一致。
6 結(jié)語
基于多體系統(tǒng)理論對三軸數(shù)控機床的幾何誤差進行劃分,建立了拓撲結(jié)構(gòu),揭示了各個體之間的關(guān)系,進而推導(dǎo)出三軸數(shù)控機床的空間誤差模型,并利用三坐標測量機和在機測量系統(tǒng)分離出幾何誤差。
136-0043-0755
